こんにちは、hokkyokunです。
私は資産形成をインデックス投資信託のクレカ積立で行っています。
今まで一度も資産の取り崩しをシミュレーションしたことがなかったので、Pythonを使ってやってみようと思います。
金融のシミュレーションにはモンテカルロシミュレーションが良いとのことですので、
これを用いてやっていきます。

モンテカルロ法とは
モンテカルロ法について調べてみました。
モンテカルロシミュレーションは、確率的なプロセスやシステムを理解し、予測するための強力な手法です。ランダムサンプリングや確率分布を用いて、実世界の不確実性を持つ現象を数値的にシミュレートします。この手法は、ファイナンス、物理学、工学、プロジェクト管理など、多岐にわたる分野で広く応用されています。
株価などランダムに動くけどあるていど傾向がみられるものに対し、乱数を生成させてシミュレートするのに使うみたいです。
ここでは株価の予測をすることを目的に手法を組み立てます。
- 株価リターンは正規分布すると仮定する
つまり、平均リターン付近に多く集まり、低すぎるリターンや高すぎるリターンはめったにない、平均から遠くなるにつれて起こる回数も少なくなる。 - 平均リターンとボラティリティを指定することで
正規分布の形を指定する。 - そこから乱数をとり、仮想のリターンを設定し、運用のシミュレーションを行う。
平均リターン7%、ボラティリティ(変動率)15%の正規分布を考えてみます。
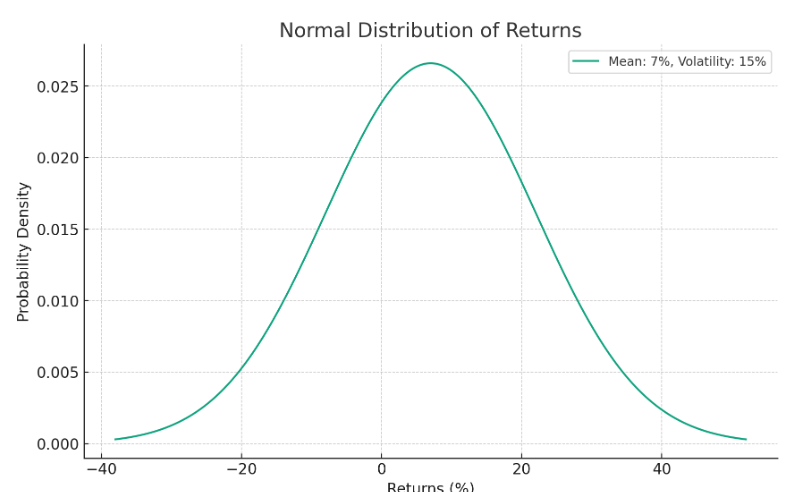
こんな感じの図が描けます。リターンが7%付近のパターンが非常に多く、それより極端に大きいリターンも小さいリターンも少なくなります。
次に平均リターン3%、ボラティリティ5%の場合を見てみましょう
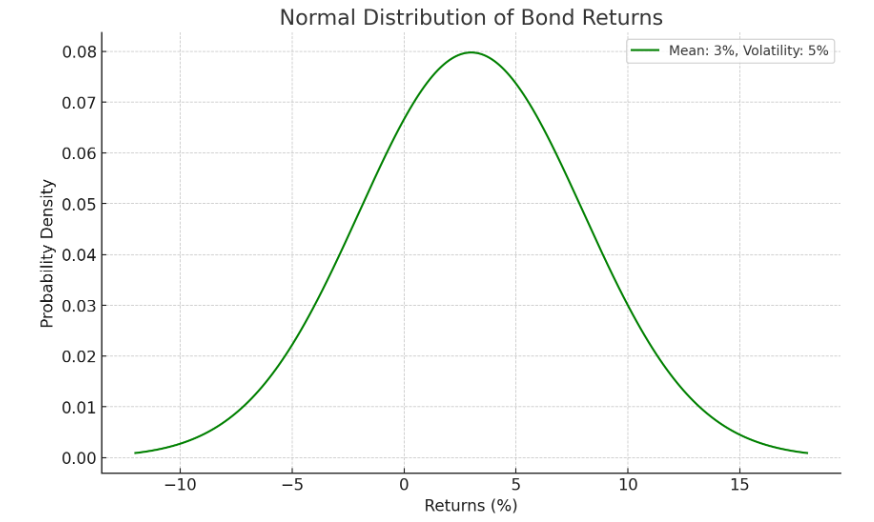
縮尺の問題でわかりずらいので、同じグラフにしてみましょう
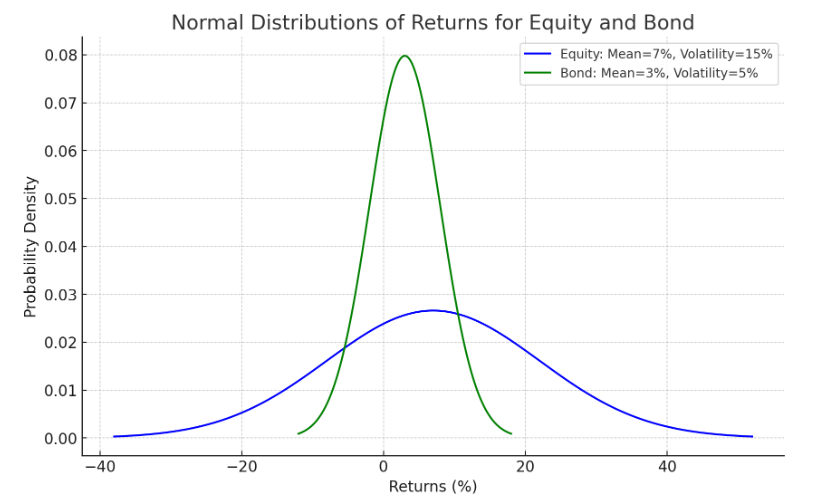
平均リターン7%、ボラティリティ15%が青、
平均リターン3%、ボラティリティ5%が緑です。
同じ正規分布でもばらつきが全然違いますね。
平均リターンと、ボラティリティを指定して、正規分布から乱数をとり、リターンとしてシミュレーションします。
ところでお気づきになりましたでしょうか
平均リターン7%、ボラティリティ15%は一般的にS&P500の数値といわれています。


平均リターン3%、ボラティリティ5%は債券ETFの代表格であるAGGのスペックです。


コード
Pythonコード
引数の説明
initial_capital: 初期資産額。シミュレーション開始時の投資ポートフォリオの価値です。expected_return: 期待リターン。年率で表され、投資ポートフォリオが将来にわたって得ると予想される平均的な収益率です。volatility: ボラティリティ。年率で表され、投資リターンの変動の大きさを示す指標です。リスクの尺度とも考えられます。withdrawal_amount: 年間取り崩し金額。各年に投資ポートフォリオから取り崩す金額です。years: 取り崩し年数。シミュレーションを行う総年数です。- seed:乱数のシード値(指定すると毎回同じ乱数になる。パラメータを変えて検証するとき便利)
戻り値の説明
dfで返ります。
以下の列を含みます。
- 年:取り崩してからの経過年
- 取り崩し額:年間の取り崩し額
- リターン:取り崩し後の残高に期待リターンをかけます。所謂収支です。
- 残高:取り崩し後、運用益を加えた資産残高です。
def simulate_withdrawals(initial_capital, expected_return, volatility, withdrawal_amount, years,seed=None):
#初期設定
capital = initial_capital
# シード値の設定
if seed is not None:
np.random.seed(seed)
datas=[]
for i in range(years):
year = i+1
#乱数でリターンを決定
annual_return = np.random.normal(expected_return,volatility)
#取り崩し
capital -= withdrawal_amount
#リターンの計算
return_amount = int(capital * annual_return)
#残高計算
capital += return_amount
datas.append([year,withdrawal_amount,return_amount,capital])
#残高がマイナスになったら試合終了
if capital < 0:
print("資産が底をつきました")
break
columns = ["年","取り崩し額","リターン","残高"]
df = pd.DataFrame(datas,columns=columns)
return df実際に使ってみます
実際に使ってみます。
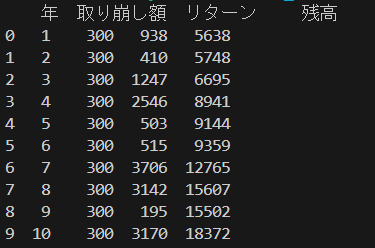
平均リターン7%、ボラティリティ15%の結果です。
ちょっと短いですが10年としてみます
df=simulate_withdrawals(initial_capital=5000, expected_return=0.07, volatility=0.15, withdrawal_amount=300, years=10,seed=42)
print(df)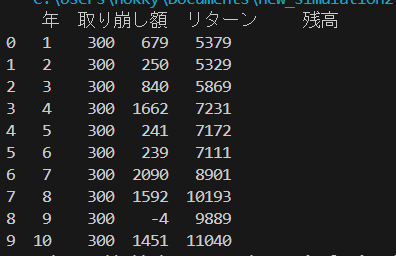
続いて
平均リターン3%、ボラティリティ5%で検証してみます。
df=simulate_withdrawals(initial_capital=5000, expected_return=0.03, volatility=0.05, withdrawal_amount=300, years=10,seed=42)
print(df)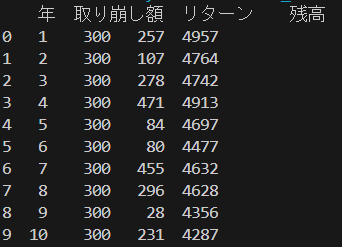
実際のデータで検証
さて、実際のデータで検証してみます。
私の大好きなVTIというETFがありますので、そちらで調べてみようと思います。
実際のOHLCVデータ(株価の始値、高値、低値、終値、ボリューム)から平均年間リターンとボラティリティを計算し、上記の関数を動かします。
def calculate_annual_return_volatility(file_path):
# データの読み込み
data = pd.read_csv(file_path)
# 'Adj Close'を用いて日々のリターンを計算
data['Daily Return'] = data['Adj Close'].pct_change()
# 年間リターンの平均値とボラティリティを計算
# 日々のリターンの平均値に取引日数を掛ける
annual_return_mean = data['Daily Return'].mean() * 252
# 日々のリターンの標準偏差に√取引日数を掛ける
annual_volatility = data['Daily Return'].std() * np.sqrt(252)
return annual_return_mean, annual_volatility金融業界では一年間の営業日数を252日で数えることが多いらしく、年間リターンを252日で計算してみました。
上記の関数を動かすとVTIの平均リターンは10.4%、ボラティリティは19.3%でした。
近年はやはりかなり高い値のようですね。